Conceitos
- Montante: é a soma do capital (Principal) com o juro relativo ao período de aplicação. Sua fórmula é S = C + j ou

- Juro Composto: é aquele que, a partir do segundo período financeiro é calculado sobre o Montante do período anterior. O Juro é composto quando a cada período os juros são incorporados ao Principal e o novo Principal passa também a render juros. Fórmula:

- Taxas Equivalentes: fazem com que o Capital produza o mesmo Montante, no final do mesmo prazo de aplicação.
- Valor Atual: chama-se valor atual de um compromisso futuro à determinada taxa de juros, ao capital que, se colocado a render jurosàquela taxa, a partir da data de hoje, atingiria um montante igual ao valor nominal do compromisso, em sua data de vencimento.
- Desconto: é a diferença entre o valor nominal (valor indicado no título |valor no vencimento|) e o valor atual (valor do título antes do vencimento).
- Desconto Racional (por dentro): é o equivalente ao juro simples produzido pelo valor atual no período correspondente, à taxa fixada.
- Desconto Comercial (por fora): é o equivalente ao juro simples produzido pelo valor nominal no período correspondente, à taxa fixada.
- Capitalização: é a remuneração de determinado capital durante um intervalo de tempo.
Conceitos básicos
Quando você vê em uma propaganda: "Compre uma televisão à vista por R$ 1 mil ou a prazo em 5 parcelas de R$ 260,00" Você, claro, responde: "A prazo, pois prefiro pagar parcelado, em poucas vezes por mês, e em apenas 5 meses eu acabo de pagar."
Mas você esqueceu de pensar em um "detalhe": 5 parcelas de R$ 260,00 perfazem o equivalente a R$ 1.300,00 – que é 30% a mais do que a oferta á vista (R$ 1.000,00). São em situações como essas que você percebe como a matemática financeira é uma ferramenta útil na análise de algumas alternativas de investimento ou financiamento de bens de consumo. Ela consiste em empregar procedimentos matemáticos para simplificar a operação financeira.
Algumas definições são interessantes para incrementar os conhecimentos sobre Matemática Financeira.
Assim, temos que o JURO, é uma compensação que se oferece à pessoa que emprestou o dinheiro, pela privação que esta pessoa está sofrendo durante o período em que ficou sem aquele capital.
Capital
O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como:Principal, Valor Atual, Valor Presente ou Valor Aplicado.
Período
Toda transação financeira deve necessariamente prever quando (datas de início e do término da operação) e por quanto tempo (duração da operação) se dará a cessão (o empréstimo) do capital. Este prazo deve estar expresso em determinada unidade de tempo (que pode ser:dia, mês, bimestre, trimestre, semestre, ano, etc.).
Exemplo: O investidor emprestou durante 3 anos o capital ao tomador.
Montante
Exemplo: “O investidor emprestou durante 3 anos o capital ao tomador, e recebeu um montante de 30% a mais do que emprestou”
Fórmulas Matemáticas
Conforme observamos no início, a Matemática Financeira pode nos auxiliar no estudo financeiro, a partir desse ponto utilizaremos a seguinte notação:
- C ou P= capital ou principal;
- J = juro;
- i = taxa de juro;
- M = montante;
- n[nota 1] = número de períodos.
- Exemplo: M = C + J
Juros
Juro é uma remuneração ou taxa cobrada sobre algum recurso emprestado. Ele pode ser cobrado de duas formas: simples e composto.
Juros simples
Os juros são sempre calculados sobre o valor inicial da transação, não importando o montante final e o período.
A formula para juros simples é:
Exemplo: Um homem tem uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m. (ao mês) pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que o homem pagará serão:
Ao somarmos os juros ao valor principal temos o montante (M), de 1160,00 no caso.
Assim, temos que Juros simples é uma proporção ao capital inicial e ao tempo em que se utilizou este capital.
O juro (j) é (=) uma proporcionalidade (i) ao capital inicial (c) e ao tempo (t).
A proporcionalidade (i) é denominada de taxa de juros racional simples e é definida como a razão entre o juro obtido e o produto do capital inicial pelo tempo em que foi utilizado.
J = C x I x T;
M = C + J
M = C x ( C x I x T);
M = C x ( 1 + [I x N]);
Uma pessoa aplicou um capital de R$ 2.500,00 no regime de juros simples por um período de 10 meses e obteve no final um montante de R$ 3.250,00. Pede-se, calcular a taxa mensal de aplicação, ou seja, i.
Capital = c = $ 2.500,00 Tempo = t = 10 meses Montante= m = $ 3.250,00 Taxa = i =
logo, J = M - C
J = $ 3.250,00 - $ 2.500,00 = $ 750,00
E, J = C x I x T
$ 750,00 = $ 2.500 x i x 10i = $ 750,00 / ( $ 2.500,00 x 10) = 75 / 2500 = Dividir numerador e denominador por 25 e, ao final temos:
i = 3/100 = 3%
A taxa procurada é de 3% ao mês.
Juros compostos
Os juros de cada período de tempo é calculado sobre o saldo no início do período anterior. Ou seja:os juros de cada intervalo de tempo é incorporado ao capital inicial e passa a render juros também.
A formula para juros compostos é:
Exemplo: Um homem empresta R$1000 com juros de 10%, no outro mês deverá R$1100, e no próximo R$1210, R$1331 e etc. O juro é calculado sobre o montante principal mais os juros do período anterior.
Taxa de juros
Taxa de juro é o valor do juro expresso como percentagem de determinado capital. A taxa de juro pode ser representada de duas formas:
Forma Percentual: 5%; 1,25%; 0,04%.
Exemplo: Dada uma taxa de “10%” ao ano, então a aplicação de $ 100,00, por um ano, gera um juro de $10,00.
Forma Unitária: 0,05; 0,0125; 0,0004
Exemplo: Dada uma taxa de “0,10” ao ano, então a aplicação de $ 100,00, por um ano, gera um juro de $10,00.
Problema Clássico de financiamento
O problema clássico de financiamento possui as 6 variáveis listadas abaixo
| Sigla em Inglês | Sigla em Português | Extenso em Inglês | Extenso em Português |
| pv | vp | present value | valor presente |
| fv | vf | future value | valor futuro |
| nper | nper | number of periods | número de períodos |
| pmt | pgto | payment | pagamento (valor da prestação) |
| rate | taxa | interest rate | taxa de juros |
| type | tipo | 0 (default), se postecipada, 1 se antecipada | 0 (default), se postecipada, 1 se antecipada |
A taxa de juros (rate) com que trabalhamos é relacionada a um período, em geral mensal ou anual. Dada a taxa (rate), pode-se calcular a variável auxiliar k como mostrado na fórmula abaixo. Quando a taxa é zero (sem juros), k = 1
O problema postecipado é o mais comum. Para esse problema, vale a figura ao lado.
Para calcular vp, basta observar que ele é a soma de cada parcela de valor pmt trazida a uma taxa de juros rate pelos períodos 1, 2, ..., nper:
Aplicando a fórmula da soma dos termos de uma progressão geométrica, chega-se a:
Notas
- ↑ n indica o número de períodos ao qual os juros são aplicados. Exemplo: se a taxa é de 1% a.m., o período (n) é o número de meses que uma taxa de juros foi aplicada sobre o montante.
Desdobramentos da formula de juros:
FV = PV*(1+i)^n
PV = FV/(1+i)^n
i = [(FV/PV)^1/n]-1
n = log(FV/PV) / log(1+i)
Ligações externas
- Calculadora Financeira On-line - Versão on-line das principais fórmulas financeiras do Excel e OpenOffice Calc.
- Calculadora de Amortização - Calcula o pagamento dos juros e do principal bem como o acumulado dos juros e pagamentos.
- Calculadora HP-12C Virtual
Referência Bibliográfica
- Wikilivros - Matemática Financeira

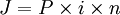
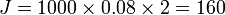
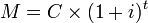





Nenhum comentário:
Postar um comentário