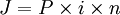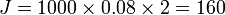Blog do Professor Vanito

I - Identificação

• Escola: EE Várzea Grande

• Professor: Vanito de Almeida Lara

• Disciplina: Matemática

• Etapa: Ensino Médio

II - Objetivo Operacional:

A partir dos dados financeiros pesquisados trazidos pelos educandos, os mesmos deverão demonstra corretamente como os juros estão sendo embutidos no preço real das mercadorias

III – Conteúdo: Juros compostos e escondidos:

No Ponto de Vista, Stephen Kanitz mostra como a máquina exigida para controlar um sistema de crédito acaba tornando o produto vendido a prestação muito mais caro do que à vista.

Por isso, ele aconselha fugir da histórica mania, estimulada pelos baixos salários da população brasileira, de se enredar nas dívidas crescentes da aquisição de bens a prazo. Muitas mercadorias, no entanto, são oferecidas sob condições convidativas mas enganadoras. Por exemplo, um artigo de consumo vendido em dez vezes "sem juros".

É evidente que de algum lugar o dinheiro deve estar saindo para financiar as prestações. Será da loja, que resolveu reduzir sua margem de lucro? Ou será que os juros já estão embutidos no preço à vista, mas não revelados para estimular a compra a prazo? Que vantagens tem o comerciante na venda parcelada? A principal é a de garantir seu mercado, uma determinada faixa de consumidor que não pode pagar tudo de uma vez.

Embora sejam aparentemente simples, essas questões devem ser formuladas na hora de optar por uma ou outra forma de pagamento. A investigação dos mecanismos para a elaboração de preços e a exata determinação das variáveis necessárias para decidir uma compra são tarefas para os quais o instrumental da Matemática é muito valioso.

IV Estratégias

•Os alunos deverão pesquisar preços de um determinado produto em duas ou três lojas com clientela de diferentes níveis socioeconômicos.

• Os alunos a registrar o maior número de dados possível: preço à vista, número de parcelas sem juros, valor das prestações e taxas de juros praticadas, ofertas etc.

• Com essas informações em mãos, passe ao exame comparativo das condições oferecidas. Chame a atenção, se possível, para os preços disfarçados de determinadas promoções. Por exemplo, quando a loja oferece brindes, mas compensa o custo deles cobrando juros maiores ou vendendo a prazo sem aumentar as taxas, mas partindo de preço à vista mais alto.

• Em seguida, tome como referência uma loja que ofereça preços iguais para compras à vista e a prazo. Simule uma situação em que os estudantes resolvem comprar a prazo um bem de, digamos, 3000 reais em 10 parcelas fixas de 300 reais e que eles investem um certo valor na poupança (taxa suposta de 0,61% ao mês), suficiente para saldar cada uma das prestações e zerar o saldo com a quitação da última parcela. Qual seria essa quantia — valor presente (Vp)?

• Mostrando as contas.

Entrada: R$ 300,00

1ª prestação: R$ 300,00

A quantia (x1) que os alunos devem aplicar hoje para saldar a primeira prestação é obtida pela expressão:

X1.(1 + 0,61%) = 300 ou x1 = 300 : 1,0061, logo x1 = 298,18

A quantia (x2) que eles devem ter hoje para pagar a segunda prestação de 300 reais vem por cálculo semelhante:

x2 (1 + 0,61%)² = 300, ou x2 = 300 : 1,0031², logo x2 = 296,18

e assim por diante.

Dessa forma, o valor presente pode ser determinado pela soma das parcelas:

Vp = 300 + 300/1,0061 + 300/1,0061² + ... + 300/1,00619 Ou, de forma simplificada:

Vp = 300.[(1/1,0061)10 - 1] : (1/1,0061 - 1)

Vp = 2919,46

Em resumo, se a turma possui hoje 2916,46 reais, levando em conta a possibilidade de aplicação com renda mensal de 0,61%, ela teria exatamente a quantia necessária para quitar a entrada e as outras nove parcelas. Como o valor presente equivale a aproximadamente 97,3% de 3000 reais, se o vendedor der um desconto maior do que 2,7% para pagamento à vista, é mais vantajoso desembolsar todo o dinheiro de uma só vez.

Caso a loja ofereça prestações sem juros nesse bem – que vale 3.000 reais -, ele está ou perdendo Pinheiro ou usando um truque, pois poderia destinar tal cifra para aplicações financieras de renda fixa a 1,6% ao mês, por exemplo. Na verdade, as taxas para investimentos podem ser até maiores. Assim, na mesma linha de raciocínio, a quantia que o consumidor precisaria aplicar hoje para cegar aos 3.000 reais em 10 meses é dada por:

Vp = 300.[(1/1,0160)10 - 1] : (1/1,061 - 1) Vp = 2796,10

Ou seja, desconsiderando os centavos, o valor presente é de 2.796 reais, o que representa um desconto de 6,8% sobre os 3.000 reais. Esse percentual poderia ser revertido para reduzir o preço do produto se o cliente optasse por pagamento integral. Assim, totais idênticos à vista e a prazo significam custo financiero que sai do bolso de alguém. De quem?

V – Avaliação:

Será considerada Satisfatória se os 5 grupos conseguirem demonstrar corretamente os juros compostos e escondidos a partir dos preços pesquisados.

Fonte: http://revistaescola.abril.com.br/ensino-medio/juros-compostos-escondidos-explore-tema-alunos-425438.shtml

Conceitos

Montante: é a soma do capital (Principal) com o juro relativo ao período de aplicação. Sua fórmula é $S = C + j$ ou $S=C(1+i \times n)$
Juro Composto: é aquele que, a partir do segundo período financeiro é calculado sobre o Montante do período anterior. O Juro é composto quando a cada período os juros são incorporados ao Principal e o novo Principal passa também a render juros. Fórmula: $J=C \times ((1+i)^n-1)$
Taxas Equivalentes: fazem com que o Capital produza o mesmo Montante, no final do mesmo prazo de aplicação.
Valor Atual: chama-se valor atual de um compromisso futuro à determinada taxa de juros, ao capital que, se colocado a render jurosàquela taxa, a partir da data de hoje, atingiria um montante igual ao valor nominal do compromisso, em sua data de vencimento.
Desconto: é a diferença entre o valor nominal (valor indicado no título |valor no vencimento|) e o valor atual (valor do título antes do vencimento).
Desconto Racional (por dentro): é o equivalente ao juro simples produzido pelo valor atual no período correspondente, à taxa fixada.
Desconto Comercial (por fora): é o equivalente ao juro simples produzido pelo valor nominal no período correspondente, à taxa fixada.
Capitalização: é a remuneração de determinado capital durante um intervalo de tempo.

Conceitos básicos

Quando você vê em uma propaganda: "Compre uma televisão à vista por R$ 1 mil ou a prazo em 5 parcelas de R$ 260,00" Você, claro, responde: "A prazo, pois prefiro pagar parcelado, em poucas vezes por mês, e em apenas 5 meses eu acabo de pagar."

Mas você esqueceu de pensar em um "detalhe": 5 parcelas de R$ 260,00 perfazem o equivalente a R$ 1.300,00 – que é 30% a mais do que a oferta á vista (R$ 1.000,00). São em situações como essas que você percebe como a matemática financeira é uma ferramenta útil na análise de algumas alternativas de investimento ou financiamento de bens de consumo. Ela consiste em empregar procedimentos matemáticos para simplificar a operação financeira.

Algumas definições são interessantes para incrementar os conhecimentos sobre Matemática Financeira.

Assim, temos que o JURO, é uma compensação que se oferece à pessoa que emprestou o dinheiro, pela privação que esta pessoa está sofrendo durante o período em que ficou sem aquele capital.

Capital

Que originou a transação ou qualquer valor expresso em moeda que uma pessoa concorda em ceder a outro, temporariamente, geralmente cobrando juros. Aquele que cede é chamado de investidor e aquele que recebe é chamado tomador. Exemplo: “O investidor emprestou o capital ao tomador”

O Capital é o valor aplicado através de alguma operação financeira. Também conhecido como:Principal, Valor Atual, Valor Presente ou Valor Aplicado.

Período

Toda transação financeira deve necessariamente prever quando (datas de início e do término da operação) e por quanto tempo (duração da operação) se dará a cessão (o empréstimo) do capital. Este prazo deve estar expresso em determinada unidade de tempo (que pode ser:dia, mês, bimestre, trimestre, semestre, ano, etc.).

Exemplo: O investidor emprestou durante 3 anos o capital ao tomador.

Montante

Montante é o valor emprestado ao tomador acrescido dos juros cobrados. Dessa forma, se é emprestado R$ 1.000,00 com juros de R$ 300,00, o montante é de R$1.300,00

Exemplo: “O investidor emprestou durante 3 anos o capital ao tomador, e recebeu um montante de 30% a mais do que emprestou”

Fórmulas Matemáticas

Conforme observamos no início, a Matemática Financeira pode nos auxiliar no estudo financeiro, a partir desse ponto utilizaremos a seguinte notação:

C ou P= capital ou principal;
J = juro;
i = taxa de juro;
M = montante;
n^{[nota 1]} = número de períodos.

Exemplo: $M = C + J$

Juros

Juro é uma remuneração ou taxa cobrada sobre algum recurso emprestado. Ele pode ser cobrado de duas formas: simples e composto.

Juros simples

Os juros são sempre calculados sobre o valor inicial da transação, não importando o montante final e o período.

A formula para juros simples é:

$J = P \times i \times n\,$

Exemplo: Um homem tem uma dívida de R$ 1000,00 que deve ser paga com juros de 8% a.m. (ao mês) pelo regime de juros simples e devemos pagá-la em 2 meses. Os juros que o homem pagará serão:

$J = 1000 \times 0.08 \times 2 = 160\,$

Ao somarmos os juros ao valor principal temos o montante (M), de 1160,00 no caso.

Assim, temos que Juros simples é uma proporção ao capital inicial e ao tempo em que se utilizou este capital.

O juro (j) é (=) uma proporcionalidade (i) ao capital inicial (c) e ao tempo (t).

A proporcionalidade (i) é denominada de taxa de juros racional simples e é definida como a razão entre o juro obtido e o produto do capital inicial pelo tempo em que foi utilizado.

J = C x I x T;

M = C + J

M = C x ( C x I x T);

M = C x ( 1 + [I x N]);

Uma pessoa aplicou um capital de R$ 2.500,00 no regime de juros simples por um período de 10 meses e obteve no final um montante de R$ 3.250,00. Pede-se, calcular a taxa mensal de aplicação, ou seja, i.

Capital = c = $ 2.500,00 Tempo = t = 10 meses Montante= m = $ 3.250,00 Taxa = i =

logo, J = M - C

J = $ 3.250,00 - $ 2.500,00 = $ 750,00

E, J = C x I x T

$ 750,00 = $ 2.500 x i x 10
i = $ 750,00 / ( $ 2.500,00 x 10) = 75 / 2500 = Dividir numerador e denominador por 25 e, ao final temos:

i = 3/100 = 3%

A taxa procurada é de 3% ao mês.

Juros compostos

Os juros de cada período de tempo é calculado sobre o saldo no início do período anterior. Ou seja:os juros de cada intervalo de tempo é incorporado ao capital inicial e passa a render juros também.

A formula para juros compostos é:

$M = C \times (1 + i)^t\,$

Exemplo: Um homem empresta R$1000 com juros de 10%, no outro mês deverá R$1100, e no próximo R$1210, R$1331 e etc. O juro é calculado sobre o montante principal mais os juros do período anterior.

$M = 1000 \times (1 + 0.10)^3 = 1331\,$

Taxa de juros

Taxa de juro é o valor do juro expresso como percentagem de determinado capital. A taxa de juro pode ser representada de duas formas:

Forma Percentual: 5%; 1,25%; 0,04%.

Exemplo: Dada uma taxa de “10%” ao ano, então a aplicação de $ 100,00, por um ano, gera um juro de $10,00.

Forma Unitária: 0,05; 0,0125; 0,0004

Exemplo: Dada uma taxa de “0,10” ao ano, então a aplicação de $ 100,00, por um ano, gera um juro de $10,00.

Problema Clássico de financiamento

O problema clássico de financiamento possui as 6 variáveis listadas abaixo

Sigla em Inglês	Sigla em Português	Extenso em Inglês	Extenso em Português
pv	vp	present value	valor presente
fv	vf	future value	valor futuro
nper	nper	number of periods	número de períodos
pmt	pgto	payment	pagamento (valor da prestação)
rate	taxa	interest rate	taxa de juros
type	tipo	0 (default), se postecipada, 1 se antecipada	0 (default), se postecipada, 1 se antecipada

A taxa de juros (rate) com que trabalhamos é relacionada a um período, em geral mensal ou anual. Dada a taxa (rate), pode-se calcular a variável auxiliar

k

como mostrado na fórmula abaixo. Quando a taxa é zero (sem juros),

k = 1

$k=\frac{1}{1+taxa}$

O problema postecipado é o mais comum. Para esse problema, vale a figura ao lado.

Para calcular vp, basta observar que ele é a soma de cada parcela de valor pmt trazida a uma taxa de juros rate pelos períodos 1, 2, ..., nper:

$\mbox{vp} = \sum_{n = 1}^\mbox{nper} \frac {\mbox{pgto}} {(1 + \mbox{taxa})^n}\,$

Aplicando a fórmula da soma dos termos de uma progressão geométrica, chega-se a:

$\mbox{vp} = \frac {\mbox{pgto}} {\mbox{taxa}} \ (1 \ - \ \frac {1} {(1 + \mbox{taxa})^\mbox{nper}})\,$

Notas

↑ n indica o número de períodos ao qual os juros são aplicados. Exemplo: se a taxa é de 1% a.m., o período (n) é o número de meses que uma taxa de juros foi aplicada sobre o montante.

Desdobramentos da formula de juros:

FV = PV*(1+i)^n

PV = FV/(1+i)^n

i = [(FV/PV)^1/n]-1

n = log(FV/PV) / log(1+i)

Ligações externas

Calculadora Financeira On-line - Versão on-line das principais fórmulas financeiras do Excel e OpenOffice Calc.
Calculadora de Amortização - Calcula o pagamento dos juros e do principal bem como o acumulado dos juros e pagamentos.
Calculadora HP-12C Virtual

Referência Bibliográfica

Wikilivros - Matemática Financeira